Your Attractive Método da Exaustão e da Bisseção:
uma análise de eficiência
TCC por Bernardo Luís Giacomelli Fernandes em 31 de Outubro de 2022
Publicado por Beatriz Pinheiro Martins
Resumo
O presente texto tem como objetivo comparar, em questão de eficiência, dois métodos numéricos que surgiram em diferentes momentos históricos: o Método da Exaustão de Arquimedes e o Método da Bisseção de Newton. Para isso, foram feitos algoritmos na linguagem de programação Python. Feito isso, optou-se por aproximar a constante π utilizando cada método e compará-los a partir disso
Palavras-chave:
Método da Exaustão de Arquimedes. Método da Bisseção de Newton. Python. Aproximação de Pi. Métodos Numéricos.
Abstract:
This text aims to compare, in terms of efficiency, two numerical methods that emerged in different historical moments: Archimedes’ Exhaustion Method and Newton’s Bisection Method. For this, algorithms were made in the Python programming language. After that, it was chosen to approximate the constant π using each method and compare them from there.
Keywords:
Archimedes’ Exhaustion Method. Newton’s Bisection Method. Python. Approximation of Pi. Numerical Methods.
1. Introdução
Métodos numéricos são um conjunto de operações matemáticas cujo objetivo é descobrir resultados com precisão arbitrária. Quando aliados à computação, utilizam a rapidez e praticidade oferecida pelo potencial de processamento dos computadores, utilizando, conforme a demanda, uma aproximação do valor a ser encontrado.
Nesse contexto, a obtenção de valores aproximados para aplicação em situações da realidade é um fato que ocorre desde a antiguidade. Arquimedes, filósofo e matemático grego, é um exemplo disso. Além de contribuições na física e astronomia, trouxe avanços na Geometria, sendo notável o Método da Exaustão, o qual estima a área de um círculo a partir da inscrição de polígonos nele, conforme mostra a Figura 1. No tempo do geômetra, a humanidade ainda não tinha o conhecimento da constante π, de fundamental importância para o cálculo envolvendo a circunferência. Graças a Arquimedes, tal valor foi descoberto, e foi estimado a partir do Método da Exaustão.
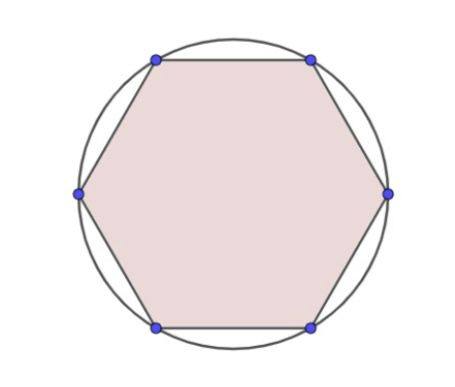
Dessa forma, as contribuições de Arquimedes não se limitam à Geometria. Exemplo disso é a contribuição do Método da Exaustão no desenvolvimento de um artifício de aproximação da área abaixo do gráfico de uma função, realizado por Bernard Riemann no século XIX. Essa estimativa é feita partir da inscrição de retângulos, de forma que a soma das áreas de todos eles seja aproximadamente a área real. Dessa forma, conforme ilustra a Figura 2, a aproximação pode resultar numa área maior ou menor do que real, a depender da quantidade de retângulos.
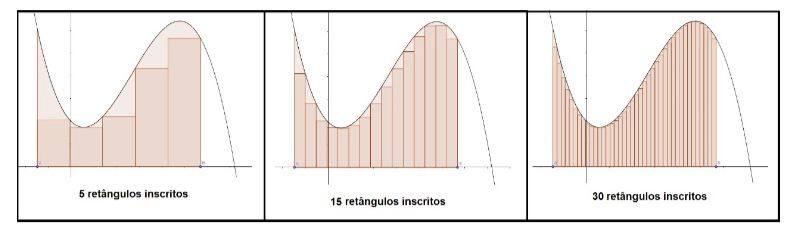
Desse modo, vários fenômenos da natureza, bem com situações práticas do cotidiano envolvem aplicações de leis matemáticas. Com efeito, a obtenção do resultado de tais expressões matemáticas é fundamental para o entendimento da realidade. As contribuições de Isaac Newton, influente físico, astrônomo e matemático, para o cálculo numérico são exemplo disso. Utilizando a ideia matemática de limite, Newton pôde desenvolver a derivação, que encontra a taxa de variação instantânea de uma função. Um outro método aproximativo desenvolvido pelo matemático foi o Método da Bisseção, concebido em colaboração com Joseph Raphson no século XVII, que obtém, a partir de um intervalo numérico, uma raiz de qualquer equação real, desde que cumpridos alguns parâmetros.
Dessa maneira, o presente texto visa verificar a aplicação de dois métodos numéricos para obter uma aproximação da constante π: o Método da Exaustão de Arquimedes, e o Método da Bisseção; bem como compará-los em questão de eficiência, agilidade e precisão. Para isso, foram construídos algoritmos para os respectivos métodos, na linguagem de programação Python.
Para a análise de eficiência de cada método, foram escolhidos os seguintes parâmetros:
• quantidade de casas decimais corretas;
• quantidade de lados do polígono necessárias ou iterações para obter tal
aproximação.
2. Método da Exaustão de Arquimedes
O Método da Exaustão de Arquimedes consiste na inscrição ou circunscrição de polígonos em uma circunferência a fim de encontrar uma aproximação da área do círculo. Para isso, calcula-se a área do polígono inscrito e a do circunscrito, e obtém-se a estimativa. Dessa forma, o erro da aproximação é dado pela subtração da área do polígono circunscrito pela área do inscrito. Portanto, quanto maior for o número de lados dos polígonos, maior é a precisão, isto é, o erro diminui à proporção que a quantidade de lados aumenta, e o oposto também é verdade (BOYER, 2012).
2.1 Explicação do Código
O código estima a área da circunferência a partir da inscrição de um polígono regular. Dessa maneira, divide-se o polígono em triângulos, que podem ser ilustrados pela Figura 3, e obtém-se a área de cada um deles.
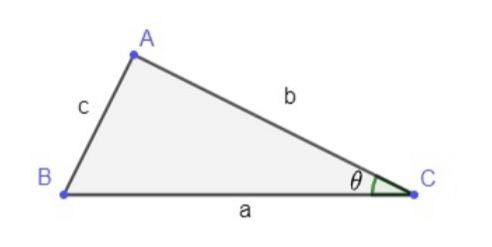
Por fim, é realizada a soma das áreas de todos os triângulos. O código parte da noção de que a área de um triângulo é expressa por:
A = a · b · sen(θ)/2,
onde a, b e c são os lados do triângulo, ao passo que A é a área.
Dessa forma, dividindo o polígono em vários triângulos congruentes, nota-se que a = b, e que ambos são iguais ao raio da circunferência (r), e calcula-se a área. Então multiplica-se o número de lados do polígono pela área do triângulo, resultando na área da figura. Por esse raciocínio, estima-se a área do círculo, escrita no código como:
A = n · r2 · sen(θ)/2,
onde n é o número de lados do polígono, θ é o parcela do ângulo central (em radianos), e r corresponde ao raio e, consequentemente, a dois lados do triângulo.
Feito isso, para obter o ângulo g, divide-se 360° pelo número de lados do polígono. Então, é feita a conversão de graus para radianos, multiplicando g por π/180 .
Nesse contexto, embora um dos objetivos do presente texto seja estimar π, esta mesma constante foi utilizada no código conforme é possível observar. Não obstante, tal limitação se deve ao fato de a conversão de graus para radianos ser possível somente por intermédio de π. Essa conversão é indispensável pois o computador calcula somente pela medida de graus em radianos.
Dessa forma, apesar de a constante ter sido aproximada por Arquimedes a partir do Método da Exaustão, na época do matemático os métodos utilizados para efetuar o cálculo eram diferentes e rudimentares. Afirma-se isso pois o geômetra utilizava uma série de polígonos inscritos na circunferência e, por causa disso, várias fórmulas específicas para calcular a área de cada um deles (BOYER, 2012). Diferentemente, o presente código calcula a área por meio das operações descritas anteriormente.
Além disso, conforme evidencia Menezes (2021), há vários polígonos que não podem ser construídos por meio de régua e compasso, mas somente pelo intermédio de computadores. Exemplos disso são o heptágono e o eneágono. Consequentemente, o código se torna um modelo aprofundado do Método da Exaustão de Arquimedes, visto que consegue calcular aproximações a partir de polígonos de quaisquer quantidades de lados.

2.2 Resultados
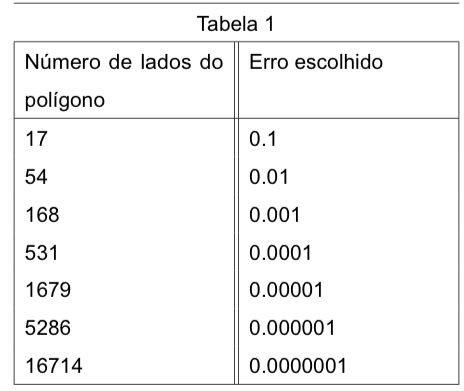
Feito o cálculo, a partir do Método da Exaustão, foi utilizada, para a verificação da quantidade de casas decimais corretas, a fórmula atual da área do círculo (πr2). Os resultados estão dispostos na Tabela 1.
Para estimar π, foi utilizado um valor de raio igual a 1. Dessa forma, obtém se um círculo cuja área é 1 · π = π.
3. Método da Bisseção de Newton
Para aplicar o método da Bisseção é necessário um intervalo numérico qualquer em que uma função f(x) intercepte o eixo x, de um plano cartesiano, somente uma vez, conforme ilustra a Figura 4. Então, calcula-se o ponto médio entre os dois números (a e b) que compõem os limites desse intervalo. O ponto médio é dado pela média aritmética de a e b (GÊVANE e CASTRO, 2010).]
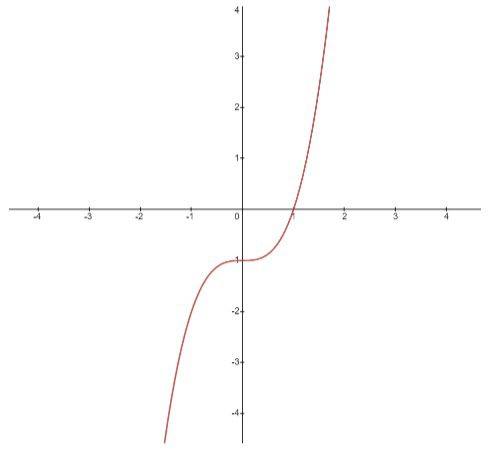
Tendo calculado o ponto médio, denominado m, calcula-se f(m). Se f(m) = 0, m é a raiz da equação. Caso contrário, f(m) pode ser maior ou menor que zero. Desse modo, tem-se que f(a) > 0, e f(b) < 0.
Então, definem-se novos limites usando o valor m. Sabemos que um dos números f(a) ou f(b) possui sinal contrário ao de f(m). Neste caso, as novas extremidades do intervalo serão (não necessariamente nesta ordem) m e o valor – a ou b – tal que a imagem dele por f tenha o sinal oposto ao de f(m).
Um detalhe notável é o fato de que para funções cuja raiz tem um valor cuja expansão decimal tem representação finita, haverá um resultado f(mn) = 0. Entretanto, há funções cujas raízes não são exatas. Nesse caso, estima-se um valor de acordo com a precisão desejada.
Outro ponto importante é a necessidade de que exista somente uma raiz no intervalo fornecido. Caso haja mais de uma, não é possível determinar a raiz (GÊVANE e CASTRO, 2010).
Para exemplificar o processo, para calcular uma raiz para f (x) = x 3 − 1, tem-se que os limites iniciais são, por exemplo, 0 e 2. Segue que:
f(0) = −1
f(2) = 7
m = 0+2/2 = 1
f(m) = f(1) = 1 − 1 = 0
Portanto, 1 é a raiz da função.
Tomando um intervalo maior, a = −1, b = 3, tem-se que:
f(a) = f(−1) = −2
f(b) = f(3) = 26 m = 2
f(m) = f(2) = 7.
Observa-se que
f(a) < 0
f(b) > 0
f(m) > 0.
Dessa forma, substitui-se b por m, uma vez que ambos possuem o mesmo sinal. Desse modo, os novos limites são −2 e 2. Então, repete-se o processo:
m2 = a+m/2 = −2+2/2 = 0
f(m2) = −1
f(m2) < 0.
Substitui-se a por m2 e tem-se que
m3 = m+m2/2 = 2+0/2 = 1
f(m3) = f(1) = 0.
Portanto, 1 é a raiz da função – o que pode ser visualizado na Figura 4.
3.1 Explicação do código
O código, para calcular a raiz de uma função em um intervalo, imita o processo descrito acima. Partindo de um intervalo numérico fornecido pelo usuário, o programa faz o processo. Uma vez que há equações cuja raiz não é exata, o programa pede o valor do erro desejado pelo usuário.
Com base nesse valor de erro, determina-se o número de iterações necessárias para obter a estimativa da raiz.




3.2 Resultados
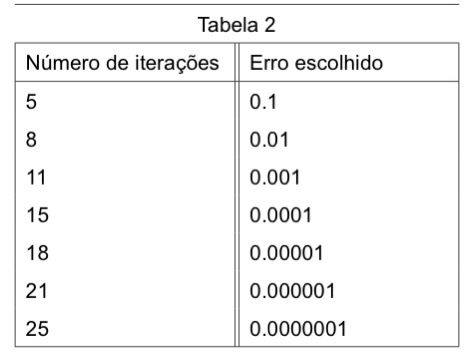
Para estimar π, foi utilizada a função f(x) = sen(x), sempre utilizando os limites de mínimo e máximo como, respectivamente, 2 e 4. Além disso, para cada aproximação, foi escolhido um valor de erro. Por meio dessa análise, foi medida a precisão da estimativa. Os resultados estão escritos na Tabela 2.
4. Comparação
Diante dos dados expostos (Tabelas 1 e 2), é possível comparar os métodos no que tange a eficiência para a obtenção de estimativas de valores.
Conforme consta na Tabela 1, o método da Exaustão precisou inscrever um polígono de 17 lados para obter uma aproximação com 0.1 de erro. Para a conseguir um erro 10 vezes menor, foi necessário um polígono 54 lados. Como se observa, a cada vez que se diminui o erro desejado em 10 vezes, multiplica-se por, aproximadamente, 3 o número de lados do polígono a ser inscrito na circunferência.
Por outro lado, quando se utiliza o método de Newton para a obtenção de π, utilizando como limites inferior e superior, respectivamente, 2 e 4, nota-se um aumento na eficiência. Para estimar o valor π com um erro de 0.1, o método utilizou 5 iterações. Para um erro de 0.01, 8 iterações. Dessa forma, a cada vez que se diminui o valor do erro desejado em 10 vezes são necessárias 3 iterações a mais, em geral.
Nesse contexto, o método da Exaustão apresenta uma progressão expressiva no que diz respeito ao número de lados do polígono inscrito. Conforme mostra a Tabela 1, para obter uma aproximação com 6 casas decimais corretas, foi necessário um polígono de 16714 lados – uma quantidade que pode ser considerada grande. A partir disso, é possível dizer que o método de Arquimedes é menos eficiente que o método de Newton, dada a quantidade de lados necessária para a aproximação.
Nesse sentido, o método de Newton apresenta uma progressão lenta quanto ao número de iterações necessárias para estimar π. De acordo com a Tabela 2, para uma aproximação de 6 casas decimais corretas, foram necessárias 25 iterações – um número que pode ser considerado pequeno. Com efeito, afirma-se que o método de Newton apresenta maior eficiência para a obtenção de aproximações, visto que possui uma menor progressão de repetições.
5. Conclusão
À face do exposto, é possível concluir que a humanidade desenvolve métodos numéricos desde a antiguidade, conforme os conhecimentos da época permitem. Dessa forma, é notável a importância do Método da Exaustão de Arquimedes para o desenvolvimento de conhecimentos algébricos e geométricos. Mais do que estimar áreas de círculos, esse método foi importante pois foi base para muitos outros métodos numéricos no decorrer da História, sendo a Aproximação de Riemman um exemplo disso.
Além disso, destaca-se o Método da Bisseção de Newton. Por meio de um intervalo numérico arbitrário, desde que cumpridos alguns parâmetros, esse método consegue calcular, ou estimar, a raiz da qualquer equação.
Nesse contexto, o presente texto teve como objetivo comparar o Método da Exaustão e o Método da Bisseção em questão de eficiência, fazendo, para isso, a estimativa do valor de π. Para tanto, foram escolhido dois parâmetros: quantidade de casas decimais corretas e a quantidade de lados do polígono inscrito ou iterações necessárias para isso.
Feito isso, observou-se que o método de Newton é mais eficiente no que diz respeito à precisão e à quantidade de iterações necessárias para o cálculo. Desse modo, ao passo que o método de Arquimedes requeria uma quantidade grande de lados do polígono para estimar π, o método de Newton precisou de uma quantidade pequena de iterações para obter um resultado com a mesma precisão.
Apesar disso, é necessário salientar que o Método da Exaustão foi criado no período da Idade Antiga, e a Bisseção na Idade Moderna, e por isso tal discrepância na eficiência é um fator justificável, dado o desenvolvimento matemático de cada período.
Desse modo, é possível observar que a matemática se desenvolveu com o passar dos séculos, e que as ferramentas antigas, embora menos eficientes que as modernas, foram de fundamental importância para a humanidade.
6. Referências
BOYER, C. História da Matemática. 3ª edição. Editora Blucher. 2012.
GÊVANE, F. e CASTRO, J. Licenciatura em Matemática: Cálculo Numérico. Fortaleza (CE). 2010.
MENEZES, C. Polígonos Construtíveis. Ouro Preto (MG). 2021
A todos que me deram apoio para finalizar este trabalho, e ao professor Papalardo pela paciência e atenção: obrigado!
