O PARADOXO DOS ANIVERSÁRIOS
Modelo Artigo Científico – TCC final por Marianna de Castro G. P. Ferreira
Resumo:
Este trabalho foi feito com o objetivo de estudar os problemas de probabilidade e, com eles, entender o paradoxo dos aniversários. Ao final, será possível perceber que, não só o paradoxo, mas muitos dados estatísticos são calculados através de modelos probabilísticos simplificados do mundo real.
Palavras-chave:
Probabilidade. Paradoxo dos aniversários. Complementar de um evento. Nascimentos.
Abstract:
This work was done with the objective of studying probability problems and, with them, understand the birthday paradox. In the end, it will be possible to realize that, not only the paradox, but many statistical data are calculated through simplified probabilistic models of the real world.
Keywords:
Probability. Birthday paradox. Complement of an event. Births.
AGRADECIMENTOS
Gostaria de agradecer ao meu professor João Papalardo que me ajudou a realizar este trabalho, e também a minha amiga e colega de TCC Maria Clara, que me acompanhou nesta jornada.
DEDICATÓRIA
Dedico o trabalho ao meu pai, que foi meu monitor de matemática quando eu era menor, e a todas as mulheres matemáticas da história que não foram ouvidas.
INTRODUÇÃO
Neste trabalho iremos analisar o estudo da probabilidade e alguns de seus paradoxos. A palavra “probabilidade” tem origem do Latim “probare”, traduzido para o português como “provar”. Ademais, é um adjetivo muito utilizado no cotidiano das pessoas para denominar um futuro que ainda não ocorreu, tendo altas ou baixas chances de acontecer ou não. Uma forma de ilustrar a teoria da probabilidade é pela metáfora do “Teorema do macaco infinito”, apresentado pelo matemático Émile Borel em 1913.
Este dispositivo abstrato afirmava que um número infinito de macacos, teclando aleatoriamente as teclas em um número infinito de máquinas de escrever por um tempo infinito, eventualmente produziria um trabalho qualquer ordenado, como uma obra literária. Essa metáfora nos faz entender que, depois de muitas tentativas fazendo algo, as chances desse algo não acontecer são mínimas.
Um paradoxo famoso do estudo da probabilidade é o chamado problema dos aniversários. Imagine-se na seguinte situação: você entra em uma sala com 23 pessoas e faz uma aposta sobre as chances de pelo menos duas delas terem nascido no mesmo dia. Todas elas vão supor que as chances são muito baixas, já que no ano temos 365 dias e naquela sala apenas 23 pessoas. E de fato faz sentido. Mas, com os cálculos de probabilidade, sabe-se que em uma sala com 23 pessoas, as chances de pelo menos duas delas terem nascido no mesmo dia já superam a marca de 50%, dado esse que poderia te levar à vitória da aposta. Mas por que isso acontece? Para que você possa responder tal pergunta durante os estudos do paradoxo, primeiro é necessário entender como a probabilidade funciona.
CAPÍTULO 1
O estudo da probabilidade é o estudo o qual, através de um cálculo, nos mostra as chances de ocorrência de uma circunstância. Para se calcular a probabilidade de se acontecer um determinado evento, deve-se calcular a razão entre casos favoráveis, a, e casos possíveis, b, respectivamente.
P(A)=a/b
Onde P é a probabilidade e A, o evento analisado.
Como exemplo, vamos resolver o seguinte problema: qual a probabilidade de tirarmos uma bola branca em uma urna que contém 10 bolas brancas e 30 bolas pretas? Para resolvê-lo, primeiro é necessário determinar os casos favoráveis e os casos possíveis.
Casos favoráveis 🡪 10 bolas brancas
Casos possíveis 🡪 40 bolas totais (10 brancas + 30 bolas pretas)
Agora que já completamos o primeiro passo, podemos passar para a última etapa, fazer o cálculo entre a razão dos dois valores.
P(A)=10/40
P(A) = 0,25
Portanto PA= 25 %. Logo, a probabilidade de tirarmos uma bola branca em uma urna com 40 bolas no total, é de 25%.
Além disso, há outras regras para se resolver problemas de probabilidade, as chamadas regras do “E” e do “OU” são utilizadas quando a probabilidade de dois ou mais eventos ocorrerem mutuamente é igual ao produto ou soma, respectivamente, das probabilidades de ocorrerem de forma separada. Para resolver exercícios deste tipo, é essencial adquirir o hábito de se perguntar “Se a situação do exercício de fato ocorreu, quais casos podem ter acontecido?” Force o aparecimento dos conectivos “e” e “ou” na sua resolução, os quais se tornam sinais e +, respectivamente. Para compreender melhor, é necessário estudar as duas formas separadamente.
Utilizando a regra do “E”
Segundo a regra do “E”, sempre que a conjunção “E” for utilizada, deve-se multiplicar as possibilidades.
Exemplo: qual a probabilidade de um casal ter dois filhos do sexo feminino?
Cenário: probabilidade de ser do sexo feminino E probabilidade de ser do sexo feminino de novo
1/2 x 1/2 = 1/4 → 25%
Utilizando a regra do “OU”
Já para a regra do “OU”, deve-se somar as possibilidades sempre que a conjunção for utilizada para resolver a questão.
Exemplo: Uma moeda é lançada uma vez, qual a probabilidade de se obter cara ou de se obter coroa?
Cenários: probabilidade de sair cara OU probabilidade de sair coroa
1/2 + 1/2 = 22 → 1
Exemplo em que as duas regras aparecem:
(Enem 2017) – Um morador de uma região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso não chova, sua probabilidade de atraso é de 25%. Para um determinado dia, o serviço de meteorologia estima em 30% a probabilidade da ocorrência de chuva nesta região. Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?
Resolução: Para resolver a questão acima, devemos fazer a seguinte pergunta: “Se o morador se atrasou para o trabalho, o que aconteceu?” A resposta é “Choveu E (X) ele se atrasou OU (+) não choveu E (X) ele se atrasou”. Transforme cada parte dessa frase na probabilidade correspondente. A do morador se atrasar quando chove, 0,5 (50100), e a dele se atrasar quando faz tempo firme, 0,25 (25100).
Cenários: choveu E ele se atrasou OU não choveu E ele se atrasou
0,3 x 0,5 + 0,7 x 0,25 =0,15 + 0,175 = 0,325 → letra c)
O complementar de um evento
Um jeito mais fácil de se descobrir qual a probabilidade de um determinado evento ocorrer é calculando o seu oposto, ou seja, a probabilidade de o mesmo não acontecer. Também chamado de método destrutivo, o complemento de um evento pode ser dado pela seguinte forma:
1- P(não acontecer)
Ex.: Uma moeda é lançada 8 vezes. Determine a probabilidade de sair pelo menos uma coroa.
Nota-se que é mais simples calcular a chance de não sair nenhuma coroa. Vamos construir um esquema onde o resultado “cara” será representado pela letra K, e coroa pela letra C.
- KKK 5- KCC
- KKC 6- CCC
- KCK 7- CCK
- CKK 8- CKC
Portanto, são 8 possibilidades. Para concluir a questão, deve-se identificar o conjunto solução que apresenta as chances de não sair nenhuma coroa.
A={KKK}
Logo, P(A)= 1/8 = 0,125. Dada a fórmula do complementar de um evento, temos que:
1- 0,125 = 0,875
Então a probabilidade de sair pelo menos uma coroa é de 87,5%.
CAPÍTULO 2
Ainda na teoria das probabilidades, muito se debate dobre o “Paradoxo dos Aniversários”, o qual afirma que dado um grupo de 23 pessoas, a chance de duas dessas terem nascido no mesmo dia é de mais de 50%. Este famoso paradoxo gera muitas surpresas em quem não o conhece, pois se o ano possui 365 dias, qual é a explicação para que em uma sala com 23 pessoas, haja mais de 50% de chances de pelo menos duas delas fazerem aniversário em um mesmo dia?
Vamos supor que 365 pessoas sejam convidadas para uma festa. Para a primeira pessoa da lista, há 365 dias possíveis com respeito à sua data de nascimento. Para a segunda também há 365 a princípio, mas apenas 364 dias para que a data não coincida com a outra. Para que a terceira não tenha nascido no mesmo dia que a primeira ou a segunda, temos 363 datas disponíveis, e para a quarta, 362. As chances de as datas serem distintas vão diminuindo. Com isso, chega-se à conclusão de que a possibilidade de pelo menos duas pessoas dessa festa terem nascido em dias iguais, vai aumentando conforme o número de convidados cresce.
Em face do que foi dito acima, veja abaixo uma tabela contendo um dado número de pessoas num grupo, e a porcentagem de pelo menos duas pessoas deste mesmo grupo terem nascido no mesmo dia do ano:
| 10 convidados | 11,7 % |
| 20 convidados | 41,1 % |
| 23 convidados | 50 % |
| 57 convidados | 99 % |
O Problema
Para solucionar o paradoxo dos aniversários e, então, achar a fórmula resolutiva desse problema, podemos começar utilizando o método destrutivo.
Exemplo: Suponha que numa sala de aula nós temos 4 estudantes. Determine qual a probabilidade de que dois deles façam aniversário no mesmo dia do ano.
Solução: Seguindo a ideia apresentada no início do capítulo, não existe restrição sobre a data de nascimento da primeira pessoa, logo, usando o método destrutivo, devemos forçar que a segunda não tenha nascido no mesmo dia que a primeira pessoa. Para que a terceira não tenha nascido no mesmo dia em que a primeira ou a segunda, deve-se forçar uma data de nascimento diferente, e assim em diante. Para essa situação, temos o cálculo:
364/365 x 363/365 x 362/365 = 0,983
⇒ 1-0,983=0,017=1,7%
Assim, a probabilidade de que, em uma sala com 4 pessoas, duas delas nasçam no mesmo dia é de 1,7%.
Repetindo o exercício acima com n=10, temos que:
364/365 x 363/365 x 362/365 x 361/365 x 360/365 x 359/365 x 358/365 x 357/365 x 356/365 =0,883
1 – 0,883 = 0,117 = 11,7%
Com isso, as chances de pelo menos duas pessoas, em um grupo de 10, nascerem no mesmo dia é de 11,7%. Veja que as chances para que dois ou mais indivíduos façam aniversário no mesmo dia do ano vai crescendo conforme aumentamos o valor de n.
Tendo em vista os exemplos acima, é perceptível que, durante o processo de resolução do problema, os numeradores da fração vão diminuindo do número 364 em diante. Com essa informação, prova-se que as contas seguem um padrão. O que nos leva até a conclusão de que, a partir disso, podemos formar uma fórmula para calcular qual a probabilidade de que em uma sala com n pessoas, pelo menos duas delas tenham nascido no mesmo dia.
Antes de entender a fórmula que deriva do paradoxo dos aniversários, é necessário entender o que é um número fatorial. Um fatorial é um número inteiro positivo o qual multiplica todos os seus antecessores até chegar ao número 1. Ademais, os fatoriais são representados por n! .
Exemplos:
1!=1
2!=2 ∙1
3!=3∙2∙1
4!=4∙3∙2∙1
E assim por diante.
Agora que entendemos o que é um fatorial, podemos seguir para a fórmula propriamente dita. Como falado anteriormente, o numerador vai multiplicando seus antecessores (363,362,361,…) à medida que a conta é feita. Por isso, conclui-se que este é um número fatorial. O mesmo acontece com o denominador da fração. Por fim, temos que:
p(n)= 365!/365ˆn x (365-n)!
Note que , para isso, despreza-se os anos bissextos.
Vimos que em uma sala com 23 pessoas, obtêm-se 50% de chances de ao menos duas delas fazerem aniversário no mesmo dia, e com 30 pessoas, esse número aumenta 20%, 70% no total. Até chegar ao número 366 em diante, valor que já consta em 100% de chances.
Observe o gráfico da função p(n), extrapolado para que tivéssemos valores para todo valor de n e não apenas n inteiro.
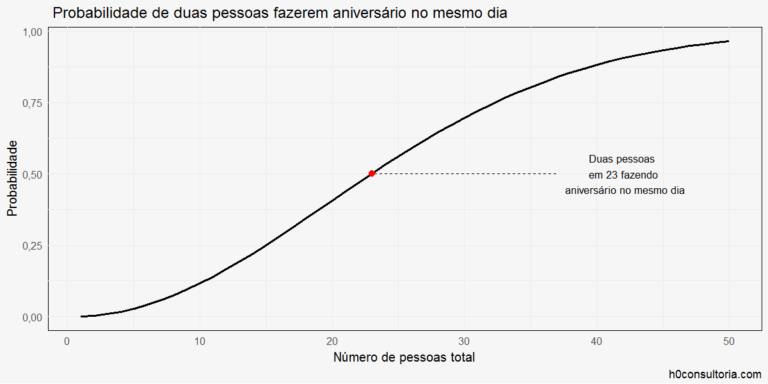
Veja como a probabilidade cresce rapidamente no início do gráfico, mas se torna mais constante em um dado número de pessoas. No Brasil, dados nos mostram que brasileiros nascem mais entre março e maio. Segundo pesquisas da BBC News Brasil, entre 1997 e 2017, ocorreram 17% mais nascimentos do que em dezembro, mês em que o número de nascimentos foi o menor nesse período. Observe o gráfico levantado pela BBC sobre o número de nascimentos por mês entre os anos anteriormente citados:
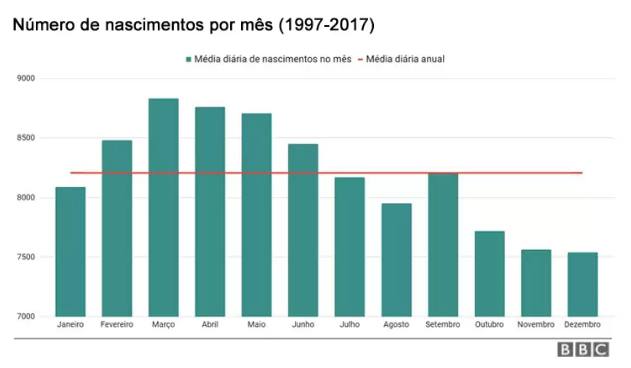
Em números exatos, são mais de 840 mil pessoas a mais. A diferença também não é de agora. Desde os anos 90, há um aumento entre os meses de março e maio, mas um declínio na chegada de novembro. Este fenômeno até hoje é muito debatido entre cientistas, mas ainda não se sabe ao certo o porquê de tal fato.
CONCLUSÃO
Veja que resolvemos um problema que, a princípio, não era de fácil aceitação. Visto que a intuição das pessoas que o enfrentam não é a de que 23 já seja um número favorável para quem faz a aposta.
Este fato é interessante do ponto de vista histórico. No contexto dos séculos XVIII e XIX, todos os estudos clássicos de probabilidade se iniciam com a ideia de entender boas estratégias e apostas em jogos de azar, tais como dados, baralho, roletas, etc. todos já foram objetos de estudos de probabilistas da época, época essa a qual marcou o início da formalização da matemática.
Foi mostrado também que para entender um fenômeno do mundo real, às vezes é necessário fazer um modelo simplificado que não o traduz de fato. No nosso exemplo, todos os dias do ano têm a mesma probabilidade de nascer um dado número de pessoas, enquanto que, na realidade, os dias são balanceados, ou seja, há determinadas datas do ano em que nascem mais pessoas e outras em que nascem menos. O que nos faz perceber que o mundo matemático deveria ter um modelo mais sofisticado para entender melhor a realidade dos nascimentos na realidade.
Em outros casos, estudos de epidemia, disseminação de doenças e o comportamento do preço do dólar são exemplos de estudos que possuem modelos simplificados, que erram com mais frequência, assim como sofisticados, que acertam com muita frequência. No entanto, todos são apenas modelos.
Com isso, é importante ressaltar que probabilidade não é prever o futuro com exatidão, mas sim uma tentativa de prever as chances de determinado evento ocorrer. O paradoxo dos aniversários é um exemplo disso, o fato de eu ter 23 pessoas numa sala não impede que nenhum par tenha nascido no mesmo dia, ainda que as chances sejam favoráveis.
BIBLIOGRAFIA
- Material de elaboração própria fornecido pelo orientador.
- https://www.bbc.com/portuguese/brasil-47269047, acesso em 11/09/22
- http://h0consultoria.com/probabilizando-o-paradoxo-do-aniversario/, acesso em 04/09/22
